
Struktura kwazikryształu jest uporządkowana, ale nie ma w niej typowej regularności. Matematyk prof. Jacek Miękisz sprawdza, jak to możliwe, że takie nietypowe ułożenie atomów może być czasami optymalne.
Kryształy lodu, soli kuchennej, cukru, ale i diamentów, szmaragdów czy kwarcu nieprzypadkowo mają piękne regularne kształty. Związane jest to z ich budową: atomy ułożone są tam bowiem w sposób bardzo uporządkowany i tworzą powtarzające się w przestrzeni wzory. Większość takich struktur daje się wpisać w wielościany, którymi bez problemu - jak cegiełkami - można wypełnić przestrzeń - układając je po prostu jedne na drugich. I tak na przykład w soli kuchennej atomy chloru i sodu rozłożone są bardzo elegancko - w rogach i na ścianach sześcianu. Jest tam więc symetria translacyjna, która sprawia, że układ powtarza się w przestrzeni, jeśli odpowiednio się go przesunie. Wydawało się, że wszystkie kryształy mają taką piękną i zrozumiałą symetrię. Do czasu, kiedy Dan Shechtman odkrył kwazikryształy.
GDZIE BRAK TRADYCYJNEJ SYMETRII
Prof. Jacek Miękisz z Uniwersytetu Warszawskiego, który pracuje nad matematycznymi modelami kwazikryształów, opowiada o badaniach Shechtmana. Ten izraelski naukowiec w latach 80. XX wieku schłodził stop glinu i manganu, a w obrazie dyfrakcyjnym ujrzał dziwną strukturę: była ona uporządkowana, ale nieokresowa: wyszedł mu układ, który miał obrotową symetrię 10-kątną. A przy takiej symetrii matematycznie niemożliwe jest uzyskanie struktury, która w sposób okresowy wypełni trój- albo dwuwymiarową przestrzeń.
WCALE NIE KWAZINAUKOWIEC
Zaobserwowanie w przyrodzie tej nieznanej wcześniej symetrii oburzyło ówczesnych fizyków. Ten sposób organizacji materii zupełnie nie mieścił się w ówczesnych "szufladkach", których używano do opisu kryształów. Shechtman spotkał się z ostracyzmem (noblista Linus Pauling grzmiał, że nie istnieją kwazikryształy, ale istnieją kwazinaukowcy). Na szczęście naukowiec się nie poddał, jego odkrycie opublikowano i uznano kilka lat później, a badacza w 2011 r. za odkrycie kwazikryształów nagrodzono Noblem z chemii. A w dodatku trzeba było tak zmienić definicję kryształu, aby objąć nią i to, co odkrył Shechtman.

Obraz kwazikryształu, Al71Ni24Fe5, znalezionego w meteorycie.
Fot. Paul J. Steinhardt et al. - http://www.nature.com/srep/2015/150313/srep09111/full/srep09111.html, Wikipedia
TAŃCZĄC NA NIEOKRESOWYM PARKIECIE
Struktura, która tak bardzo oburzyła fizyków, znana była już wtedy jednak matematykom. "Gdyby nałożyć na siebie obrazy dyfrakcyjne atomów w kwazikrysztale Shechtmana i wierzchołków w tzw. parkietażu Penrose`a - obrazy się ze sobą pokrywały" - mówi prof. Miękisz.
A parkietaż Penrose`a to bardzo interesujący układ: dwa rodzaje rombów (jeden o kątach 72 i 108 stopni, a drugi o kątach 36 i 144 stopni) z wypustkami i wcięciami wystarczają by pokryć nimi płaszczyznę, ale nie można nimi tej płaszczyzny wypełnić w sposób okresowy. W odróżnieniu do okresowych parkietaży, którymi są np. szachownica czy układ plastra miodu.
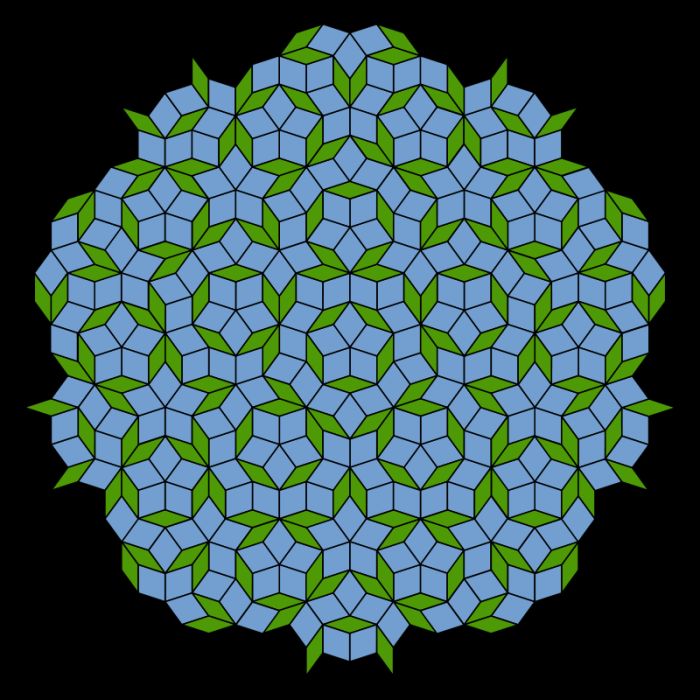
Parkietaż Penrose’a Fot: Inductiveload, Wikipedia
"Odkrycie kwazikryształów niewiarygodnie wpłynęło na rozwój matematyki, która bada struktury nieokresowe. I to w różnych jej działach: topologii, algebrze, teorii liczb" - mówi prof. Miękisz, który sam bada, co jest odpowiedzialne za to, że kwazikryształy istnieją, jaki rodzaj oddziaływań powoduje powstawanie takich struktur i czy są one odporne na ruchy termiczne.
DĄŻĄC DO OPTIMUM
Tłumaczy, że materia składa się z atomów, które oddziałują ze sobą: np. odpychają się, kiedy są zbyt blisko, a przyciągają, kiedy są zbyt daleko. Kiedy temperatura spada (w stanie równowagowym) atomy ustawiają się tak, żeby minimalizować energię. "Materia jest leniwa: chce zużywać jak najmniej energii. A jak ustawić materię, żeby energia układu była minimalna - to już zadanie matematyczne" - zauważa. Wydawało się, że dążenie do minimalizowania energii zachowane jest w klasycznych kryształach, tych o okresowej budowie. Pytanie jednak, czy to samo ma miejsce w kwazikryształach.
"Twierdzi się, że atomy w kwazikryształach układają się w taki a nie inny sposób, bo również minimalizują energię. Ale nie ma na to dowodu. A ja chcę dać tu swój wkład" - mówi matematyk. Dodaje, że aby stworzyć matematyczny model kwazikryształu, trzeba poznać siły, które łączą atomy i które sprawiają, że układają się one nieokresowo. Jego zespół chce stworzyć model, który będzie to wyjaśniał.
"Staramy się zobaczyć, jakie oddziaływania między elementami dałyby układ nieokresowy w stanie podstawowym. I czy układ ten jest odporny na zaburzenia. To dotąd problem, który w matematyce nie ma jeszcze rozwiązania" - mówi naukowiec.

Obraz dyfrakcyjny ikosaedralnego kwazikryształu Ho–Mg–Zn. Fot: Materialscientist, Wikipedia
Problematyka kwazikryształów łączy się niejako z jednym ze sławnych matematycznych problemów sformułowanym w 1900 r. przez Davida Hilberta. To problem 18. część druga. Sprowadza się on do pytania, czy istnieje bryła o takim kształcie, że możemy nią pokryć całą przestrzeń trójwymiarową w sposób nieokresowy.
OGARNĄĆ NIESKOŃCZONOŚĆ
Naukowiec opowiada, że w swoich badaniach korzysta przede wszystkim z kartki, ołówka, gumki i kosza na śmieci. Komputery w obliczeniach nie są mu więc potrzebne. "To badania z zakresu rachunków prawdopodobieństwa, układów dynamicznych, teorii miary. Komputer może to z natury rzeczy urządzenie ograniczone, a my badamy nieskończoność. Komputer może pomóc zweryfikować, jeśli nieskończoność opiszemy skończoną listą reguł. A nieskończonej liczby reguł nie zweryfikuje. Wprawdzie ludzki mózg też jest skończony, ale my już potrafimy za jego pomocą nieskończoność obejść" - podsumowuje naukowiec.
Badania realizowane są w ramach grantu Harmonia Narodowego Centrum Nauki.
PAP - Nauka w Polsce, Ludwika Tomala
lt/ agt/
Fundacja PAP zezwala na bezpłatny przedruk artykułów z Serwisu Nauka w Polsce pod warunkiem mailowego poinformowania nas raz w miesiącu o fakcie korzystania z serwisu oraz podania źródła artykułu. W portalach i serwisach internetowych prosimy o zamieszczenie podlinkowanego adresu: Źródło: naukawpolsce.pl, a w czasopismach adnotacji: Źródło: Serwis Nauka w Polsce - naukawpolsce.pl. Powyższe zezwolenie nie dotyczy: informacji z kategorii "Świat" oraz wszelkich fotografii i materiałów wideo.













