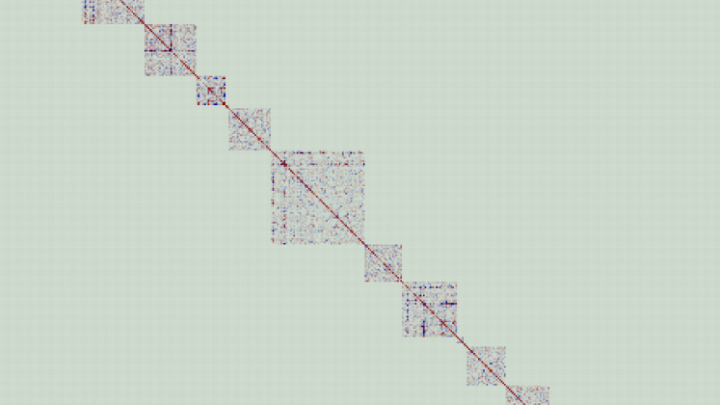
Polish mathematicians have solved a previously unsolved problem in the field of geometric group theory. Using a computer to search for matrices with specific parameters, they found the figure showed the 4641x4641 matrix presented in graphical form - the green points are 0, and the colour and its intensity correspond to the absolute value of the given matrix coefficient. Credit: M. Kaluba, D. Kielak, P. Nowak, Annals of Mathematics
Polish mathematicians have solved one of the greatest challenges of geometric group theory. Their work is about ‘symmetries of all symmetries’.
Publishing their findings in the prestigious mathematical journal, Annals of Mathematics Dr. Marek Kaluba (Adam Mickiewicz University and Karlsruher Institut fur Technologie), Professor Dawid Kielak (University of Oxford) and Professor Piotr Nowak (Institute of Mathematics of the Polish Academy of Sciences) solved the decades-old problem by showing that an infinite family of algebraic objects - groups - has property (T), and therefore is incompatible with Euclidean geometry.
Dr. Marek Kaluba said: “Thanks to our research, we have understood certain geometric aspects of the groups that code the symmetries of all symmetries.”
WHAT THE RESEARCH IS ALL ABOUT
The objects with property (T) have very exotic geometrical properties (they cannot be realized as symmetry in Euclidean geometry). Out of touch with reality? Seemingly yes. But the knowledge of this complicated property (T) has already found applications. It allows, for example, to construct expanders - graphs with a large number of connections used, for example, in streaming algorithms. Such algorithms are responsible for identifying trends on Twitter.
Professor Nowak said: “The question of whether the groups we studied have property (T) appeared in print in the 1990s. When I was a PhD student, it was a problem that I heard about at every other group theory lecture and conference.”
Dawid Kielak continued: “Our result explains the functioning of a certain algorithm. This is the Product Replacement algorithm used when you want to randomise elements from huge sets, e.g. with more elements than the number of particles in the Universe. This algorithm has existed since the 1990s and works much better than expected. Our article explains why it works so well.
“Computer science is the new physics. What surrounds us are not only molecules, but more and more often also algorithms. Our task as mathematicians will therefore be to understand algorithms, show why they work or not; why they are fast or slow.”
THE COMPUTER HELPS SEARCH FOR PROOF
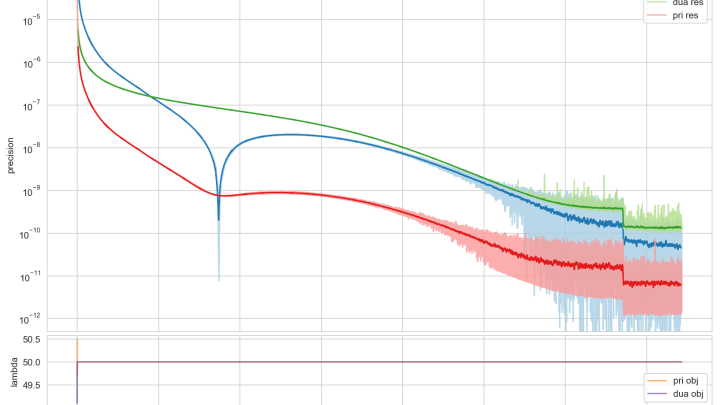
In their mathematical proof, the scientists used computer calculations to find the so-called matrix that meets certain criteria. The machine would create a solution, check how well it fulfilled the given conditions, and gradually improve the matrix in order to get to the lowest possible error rate. The only question was how low error rate it would be able to achieve.
Professor Dawid Kielak said: “The computer only did the tedious work. It did not replace logic. Our idea was to apply the reduction of an infinite problem to a finite problem.”
Dr. Marek Kaluba added: “We reduced our problem to an optimisation problem, and then used standard tools for this optimisation - algorithms that engineers use to design structural elements.”
The computer was optimising, and mathematicians, unaccustomed to the machine doing the work for them, wanted to know the error rate every few minutes. At one point, to stop his colleagues from bugging him with questions, Dr. Kaluba even set up a Twitter account that showed them what the computer had calculated on an ongoing basis.
The waiting paid off. It turned out that the computer's error in the last approximation was very, very slight. Thus, using appropriate mathematical arguments, computing allowed the scientists to obtain the exact proof.
Dr. Kaluba said that because the problem they were working on was initially too big to be solved with even a supercomputer, “we used the internal symmetries of this problem to facilitate the search for a solution.
“These symmetries (in algebraic form) can also be observed in the optimisation problem and be used to reduce complexity. So although we deal with abstract mathematics, we want our software to also be useful in engineering applications’.
Professor Piotr Nowak is one of the few Polish winners of an ERC grant. He said: “When I applied for a grant, I would not have dared to propose a solution to the problem that we have just solved. It seemed to me that nobody saw such a possibility on the horizon at that time.”
PAP - Science in Poland, Ludwika Tomala
lt/ ekr/ kap/
tr. RL
Przed dodaniem komentarza prosimy o zapoznanie z Regulaminem forum serwisu Nauka w Polsce.
