Knot a problem! When faced with the unsolvable enjoy it, says Knot Theory scientist

Getting lost when trying to solve a problem could be helpful as it can benefit research, says a Warsaw academic.
Dr. Maciej Borodzik, a mathematician specialising in knot theory at the University of Warsaw told PAP that although some knots can be untied, others can be transformed into a form we know better, while some simply cannot be untied unless we cut or cheat. The same is true for the problems we encounter in everyday life.
NOT EVERY KNOT IS GORDIAN

A problem that seems impossible to solve is not always so complicated. Fig. Kuchtact / CC BY-SA
According to Dr. Borodzik, sometimes problems that cannot be solved can be confused with very difficult ones. He said: “It happens sometimes that a person sits in front of a blank page and cannot write anything for a month. Or a year. He or she does not see the way. This usually happens when writing a doctoral dissertation. Many people quit. But - at least in mathematics - this +swamp+ stage is necessary to conduct good research. Then a person develops and begins to see the way ahead.”
DEAD END STREETS HELP SEE THE WAY OUT
He added: “There are many ways to approach a problem in mathematics, but some of them lead us astray. However, even if it is not possible to solve the problem, time spent wandering does not have to be time wasted, because the person can learn a lot.
“That is when you learn and test the ways of thinking and tools that can be useful in the next stages of work. So even if these failed ideas will not be useful in pursuing one goal, they may be useful in achieving the next ones.”
This means that even patiently trying to untie a Gordian knot can make more sense than cutting it.
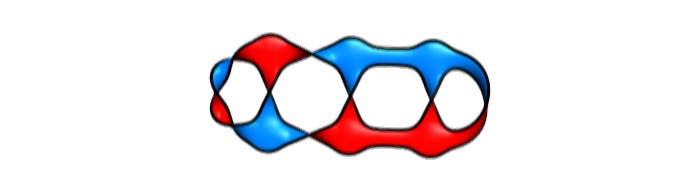
Seifert's surfaces bounded by a knot. Illustration made with free SeifertView software
KNOTS WITHOUT LIMITS
When you are trying to solve a problem, it may turn out that there are many right ways to achieve one goal. “And knots have everything - you can use methods from a very wide spectrum of mathematics,” he says.
Coming from a branch of mathematics called the singularity theory ('it is about spaces that have 'corners', he explains), in some places, his in-depth knowledge of this 'singular' field gives him an advantage over researchers who do not have this background.
ARRANGE THE KNOTS OF CIRCUMSTANCE
Recalling a problem he got stuck on for weeks, Borodzik says it was only until he asked someone about it at a science conference who happened to know the right methods, that he was able to figure it out in a few minutes
He said: “Even conversations about stupid things sometimes materialize: sometimes they turn into a big project, sometimes into fast work.”
 . Fig. collage with AnonMoos images, public domain
. Fig. collage with AnonMoos images, public domain
WHY STUDY KNOTS
“In mathematics, knots are of fundamental use in understanding 3- and 4-dimensional geometry. If a knot is cut out of space and then pasted differently, you get a curved space. All three-dimensional curved spaces can be obtained with such an operation - or a series of them.”
In such curved spaces, things that are very strange by our standards can happen. It may turn out, for example, that if two people walk in the same direction along the same straight line, they will travel completely different paths and end up in the same place at different angles. Such curved spaces may exist somewhere in the Universe, for example near black holes. Thanks to the knot theory, there will be a method to describe them.

Seifert surfaces are surfaces whose boundaries are knots. Image obtained with the free SeifertView software
HUNGRY FOR KNOWLEDGE AND PRETZELS
Solving complex math problems would not be so appealing if it were not for the feeling you get when you come up with an idea and start seeing the way to your goal.
Borodzik said: “Sometimes, when I catch a trail, I only focus on one thing. I put other topics aside, I ignore paperwork deadlines. I just feel that it is necessary.
“This feeling is similar to the emotion that accompanies reading a detective story, an addictive book. Only it is much more intense.” He added that sometimes when he gets up in the morning and wonders which project to work on that day, he feels a bit like a glutton peeking into the fridge. “It's addictive. There is a form of gluttony in it,” he says.
A KNOT VIEW
To give a taste of what evokes such emotions in mathematicians dealing with knot theory, the scientist says that knots are the most difficult to untie in 3- and 4-dimensional spaces. In spaces that have at least 5 dimensions, you can use a certain mathematical trick (Whitney's trick), which helps to describe any curvature of a space using algebraic operations. Borodzik said: “This trick works in a space that has five or more dimensions. But in a three-dimensional or four-dimensional space, it does not. The reality that we are used to perceiving with our senses is therefore much more 'tangled' than if we perceived more dimensions.”
In his research, Dr. Borodzik is particularly interested in the problem of a knot drawn on a 3-dimensional sphere, wondering, for example, what surface it bounds in four dimensions.” He adds that mathematicians have not yet found a solution to this problem despite several decades of research. And paradoxically, questions about fairly simple objects, such as spheres, are more difficult.
Examples of knots. Fig. collage with AnonMoos images, public domain
DO NOT GET ATTACHED TO ALL YOUR IDEAS
According to Borodzik, ideas do not always turn out to be right. So it's not always worth getting attached to them. He said: “First, I write my paper. And I write it incorrectly. And then I correct it. Between the first version of the paper and the last version, there are so many changes that sometimes only some dots and commas survive. But this does not mean that the first version of the paper is not needed. It is! Without it there would be no second version!
A KNOT OF FIELDS
“Mathematics deals with problems that only mathematicians are interested in. But every once in a while someone finds that an area is needed to solve other problems.”

Seifert surfaces are surfaces whose boundaries are knots. Image obtained with the free SeifertView software
One example is that in nature knots can appear in a DNA chain. If they do, there may be a problem with the production of a protein.
Scientists from various fields of science use different ways of thinking, find different pleasures in their work, and talk about their research differently, for example in scientific publications. So when they look at the same knot, they see something completely different. And this is a problem in the development of interdisciplinary research, which for now also appears to be a Gordian knot.
PAP - Science in Poland, Ludwika Tomala
lt/ zan/ kap/
tr. RL
Przed dodaniem komentarza prosimy o zapoznanie z Regulaminem forum serwisu Nauka w Polsce.



















