Microwave networks - a new tool for analysing quantum graphs
 Source: Institute of Physics PAS
Source: Institute of Physics PAS
Quantum graphs can be experimentally simulated by classical microwave networks, shows research conducted at the Institute of Physics of the Polish Academy of Sciences. This idea will allow to study quantum systems, difficult to investigate in laboratories or on supercomputers.
Solving many problems in physics poses fundamental difficulties related to computational complexity. Conventional computers, including supercomputers, are insufficient to solve complex mathematical problems related to the quantum description of matter, or to simulate quantum systems, even with only 30 particles. Better methods and computational tools are needed, for example, to understand and rationally design new materials, whose properties often depend on the collective behaviour of hundreds or thousands of quantum particles, or to design new devices in nanotechnology.
For some time, such tools have been quantum simulators, which allow to study quantum systems, difficult to study in a lab and impossible to model with a supercomputer. In this case, simulators are special purpose devices designed to provide insight into specific physical phenomena.
Quantum simulators have been implemented on many experimental platforms, including systems of ultracold quantum gases, photonic systems and superconducting circuits. One of the mathematical tools for modelling, researching and constructing simulators are quantum graphs, which, among other things, enable the creation and formal analysis of models and phenomena in mesoscopic physics used to obtain theoretical understanding and development of nanotechnology.
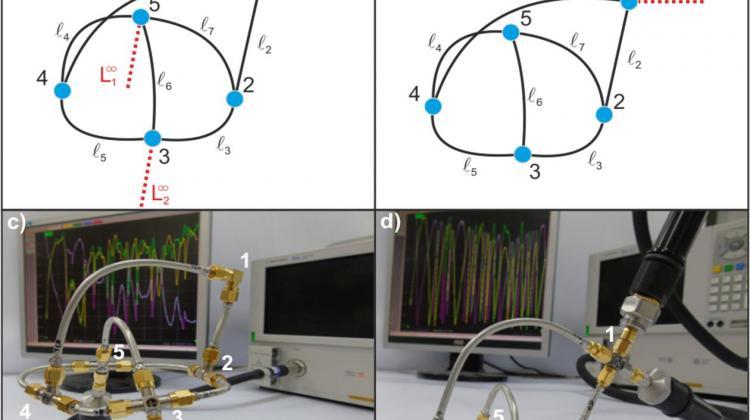
In mathematics, a quantum graph is a linear, network-shaped structure of vertices connected on edges with a given length. A practical example of such a graph is an energy network consisting of transmission lines (edges) connected in transformer stations (vertices). Differential equations would then describe the voltage along each line (edge), along with the boundary conditions for each vertex, ensuring that the current added at all edges is summed to zero at each vertex.
Quantum graphs were first studied by Linus Pauling, an American physicist and chemist and winner of two Nobel Prizes, as models of the dynamics of free electrons in organic molecules such as naphthalene. The graphs also appear in various mathematical contexts, for example as model systems in quantum chaos, in waveguide network research, in photonic crystals and in the description of the Anderson localization phenomenon.
Quantum graphs are used as idealization of real physical networks, and their most unusual properties include isospectrality. Namely, it has been shown that there are graphs of various shapes that have exactly the same spectrum of energy states. This means that the various physical systems that can be described by isospectral graphs will have similar properties.
In the real world, graphs are not closed systems, in other words they have open, unfinished edges, which make the analysis of such graphs much more difficult. For this analysis, physicists use classical simulators of quantum graphs in the form of microwave networks.
In groundbreaking research conducted at the Institute of Physics PAS, scientists have shown that quantum graphs with symmetry and without symmetry due to the time reversal can be experimentally simulated by classical microwave networks (https://doi.org/10.1103/PhysRevE.69.056205). These networks can also be used to study systems with very strong dissipation (where energy is dispersed). Since microwave networks can simulate quantum wires and many other structures, the proposed research also deepens our knowledge of the properties of these systems, which is very important from the perspective of basic research as well as future applications.
In an article that appeared in the prestigious journal Physical Review Letters (https://doi.org/10.1103/PhysRevLett.122.140503), the Polish-Czech team of authors from the Institute of Physics PAS and the University of Hradec Králové presented an important result: the first experimental implementation of graphs other than Weyl graphs. Such graphs are not characterized by the Weyl law, which describes the average density of resonances based on their total length. Using microwave networks that simulate quantum graphs, researchers have shown that there are graphs that do not correspond to the Weyl law characteristics.
"At the Institute of Physics, we demonstrated for the first time that the transition from Weyl graph to non-Weyl graph occurs if we introduce a balanced vertex, in which the numbers of connections with the outside world and internal edges are the same" - emphasises team leader and co-author of the paper Prof. Leszek Sirko. Research shows that the number of measured resonances can significantly depend on the way in which the measured system is connected to the outside world.
A similar problem arises in the case of networks built of quantum waveguides. They are mesoscopic systems built of paths with nanometer widths. According to the authors of the paper, in the description of such a system, the spectrum of the Laplace operator matches the spectrum of the Laplace operator of an analogous quantum graph modelled by their microwave networks. Therefore, a better understanding of the properties of the models built from their microwave networks should allow to create new subtle tools for quantum nanotechnology, which will allow to modify the properties of quantum structures without the need for their internal reconstruction. Such structures should simply be properly connected to the surrounding world, researchers from the Institute of Physics PAS say.
PAP - Science in Poland
lt/ ekr/ kap/
tr. RL
Przed dodaniem komentarza prosimy o zapoznanie z Regulaminem forum serwisu Nauka w Polsce.















