Dr. Achinger: In mathematics, the proof does not have to be beautiful. It`s important that it works
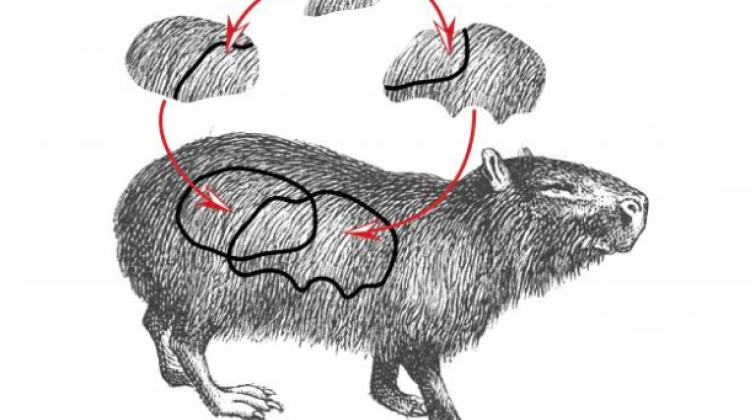Sometimes in mathematics there are algebraic varieties so complex that in order to be able to say something about them, they have to be broken down into smaller, easier to describe parts. Source: KAPIBARA project, Piotr Achinger
There are proofs in mathematics that are beautiful. But sometimes we can not prove a theorem beautifully and it is enough that the proof works - says an ERC grant laureate, mathematician Dr. Piotr Achinger. He talks about his research in the field of algebraic geometry.
Dr. Piotr Achinger from the Institute of Mathematics of the Polish Academy of Sciences specialises in algebraic geometry. In the last distribution of prestigious European Research Council (ERC) grants, the scientist received an ERC Starting Grant worth over 1 million euros. He will use these funds to carry out the project KAPIBARA and employ 6 people to help him in his research.
The mathematician is in the group of four Polish researchers who received funding in this call.
(FIELDS) MEDAL WINNING BRANCH OF MATHEMATICS
Asked about the project`s acronym KAPIBARA, Dr Achinger responds: "In my work I deal with the so-called K(π,1) spaces, so I thought about capybara. Capybara is a nice creature, easy to remember".
The scientist talks about the area of mathematics that his research concerns. "Algebraic geometry is a quite extensive branch of mathematics, which has connections with mathematical physics, differential geometry, and, on the other hand, with the theory of numbers" - he says.
As he explains, the area of mathematics he deals with is quite large and popular. "In the last award of Fields` Medals (the world`s most prestigious awards for mathematicians - PAP) out of the four awarded medals, three were related to my field. This could be an anomaly in the history of this award, but algebraic and arithmetic geometry research has been really popular since the 1970s" - he says.
COMBINING THE BRANCHES
Dr. Achinger`s research topic is quite hermetic. As he says, even professional mathematicians find it difficult to explain what his research is about. "An example problem that interests me is the description of homotopy types of algebraic varieties with positive characteristics" - says the scientist. And it decomposes the complicated sentence into prime factors.
He explains that the algebraic variety is a geometric object described by polynomial equations. For example, the equation x2+y2=1 describes the circle.
But in mathematics there are algebraic varieties that are much more complicated than the circle. To be able to say something about them, sometimes they have to be broken down into smaller, easier to describe parts.
Dr. Achinger is especially interested in those varieties that have so-called positive characteristics. "We are thinking about solutions of equations in finite number systems, for example in remainders from dividing integers by 5" - he says. "It turns out that such seemingly primitive numerical systems can also be used to carry out geometric reasoning".
HOLES WITH LOOP
In turn, "homotopy types" are associated with the description of the geometric shape of space. "Two geometrical objects can be considered equivalent, if one can be deformed to obtain the other. It is said, for example, that a cup with an ear can be transformed into a torus. This is a topological equivalence, and homotopic equivalence is even rougher" - he says.
The basic tool for describing the shape and space in algebraic topology is the basic group. "It tells us what loops can be created in a given space" - says the mathematician. He points out that in a torus (the shape of a perfect donut with a hole) there are two different loops. One goes horizontally around the donut and its hole, and the other - vertically around the narrow edge. "In the two-dimensional sphere, all the loops are the same, because we can continuously deform them and transform them into each another" - the scientist says. Mathematicians say that they are simply connected. "They do not have interesting loops" - comments the researcher.
However, if we take into account manifolds with positive characteristics, that is, those whose solutions are countable, such a search for different loops is no longer obvious. "In positive characteristics, even a straight line, a circle or a sphere are rarely simply connected, they have a lot of different weird +loops+" - says the mathematician.
The ERC awarded over 1 million euros for the research project devoted to these problems.
IT WORKS? THAT`S BEAUTIFUL!
Asked whether beauty is important in mathematics and whether he likes the proofs of his theorems, the researcher from the Institute of Mathematics PAS answers: "Sometimes, yes, there are some proofs that are beautiful. And some are not - sometimes the proof simply works, although it is not that beautiful. And we can not prove the theorem more beautifully".
FIGHT FOR A GRANT
Dr. Achinger says that applying for ERC grants is a big effort. "It`s not that I click on something on my computer a couple of times and send an application. Applying for a grant negatively affects my academic work" - he says. He says that it took him two months to prepare a grant application. And then he spent another month preparing a presentation that he had to give before the panel of experts evaluating the applications in the second round of the competition.
The ERC has awarded over 8,000 grants since 2007. Of these, Poland won just about 30, while, for example, Greece obtained 60 grants, Spain - more than 500, and France - over a thousand.
PAP - Science in Poland, Ludwika Tomala
lt/ ekr/ kap/
tr. RL
Przed dodaniem komentarza prosimy o zapoznanie z Regulaminem forum serwisu Nauka w Polsce.
