Dr hab. Szczytko: matematyka jest jak język smoków, w którym nie da się skłamać
 Drzeworyt "Smok" japońskiego artysty Hokusai Katsushiki (1760-1849). Źródło: Wikipedia
Drzeworyt "Smok" japońskiego artysty Hokusai Katsushiki (1760-1849). Źródło: Wikipedia
Matematyka jest jak język smoków, w którym nie da się skłamać. Jeśli z języka potocznego przełożymy na ten język pewne problemy, np. dotyczące zjawisk w przyrodzie, od razu widać, czy coś jest prawdą, czy fałszem - porównuje w rozmowie z PAP dr hab. fizyk Jacek Szczytko z Uniwersytetu Warszawskiego.
"W cyklu powieści Ursuli Le Guin o Ziemiomorzu przedstawiona była koncepcja języka, którym porozumiewały się smoki. One mogły w tym języku wypowiedzieć wszystko. Jeśli jednak to człowiek nauczył się języka smoków, nie był w stanie w nim skłamać - mógł mówić tylko prawdę" - przypomina w rozmowie z PAP fizyk dr hab. Jacek Szczytko z Wydziału Fizyki Uniwersytetu Warszawskiego. Według niego takim językiem smoków, w którym nie da się skłamać, jest matematyka.
"W szkole na lekcjach fizyki czy chemii, uczymy się tłumaczyć pewne problemy z języka potocznego na język matematyki" - mówi dr Szczytko. Dzięki temu można np. otrzymać wzory opisujące ruch jakiegoś ciała czy wzory reakcji chemicznych. "A w języku matematyki, tak jak w języku smoków, od razu widać, czy to, co powiedzieliśmy, to prawda czy fałsz" - porównuje. Jeśli bowiem przeprowadzimy rozumowanie zgodnie z regułami - gramatyką języka matematyki - okaże się, czy hipoteza, którą stawiamy, jest fałszywa. Jedna strona równania albo wynosi tyle samo, co druga, albo nie.
Badacz z FUW wymienia, że znaczenie "smoczego języka" doceniają nie tylko fizycy czy chemicy, ale również ekonomiści, inżynierowie, genetycy czy socjologowie, nie wspominając o informatykach.

Smoki inspirują matematyków. Smok Hartera-Heighwaya to fraktal, którego znać mogą choćby czytelnicy powieści "Park Jurajski" Michaela Crichtona). Źródło: Wikipedia, domena publiczna
SZALONY ŚWIAT KWANTÓW UJĘTY W SZTYWNYCH RÓWNANIACH
Porównanie języka smoków z matematyką zyskuje jednak szczególne znaczenie w przypadku mechaniki kwantowej - wskazuje dr Szczytko. Tam bowiem dzięki językowi matematyki możemy uzyskać dostęp do idei, które są prawdziwe, choć wyrażone w języku potocznym wydają się całkowicie nonsensowne.
Naukowiec podaje przykład odkrycia przez Maxa Plancka równań, które podpowiadały, że światło ma charakter korpuskularno-falowy: ma więc i cechy cząstki, i fali. Z takim faktem wyobraźnia słabo sobie radzi, dlatego Planck wahał się, czy ogłosić swoje odkrycie światu. Dwoistość natury światła - która ukazała się ludzkim oczom najpierw w "języku smoków" - okazała się jednak później prawdziwa w eksperymentach. A z czasem znalazła także praktyczne zastosowania (efekt fotoelektryczny wykorzystywany jest np. w bateriach słonecznych czy noktowizorach).
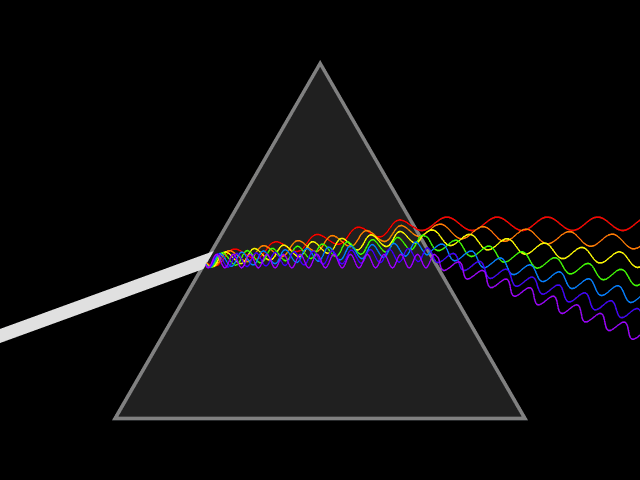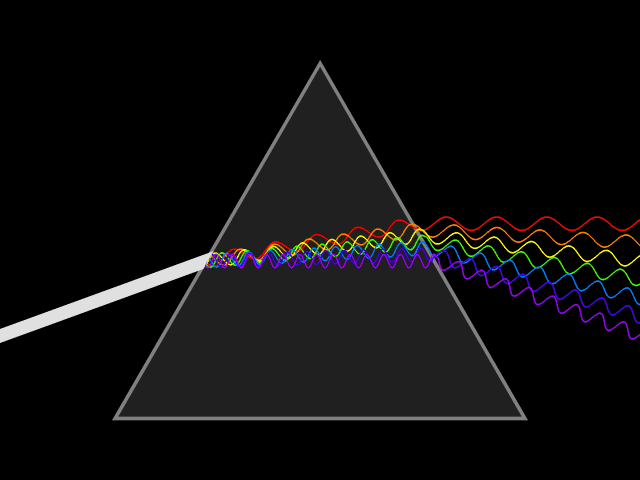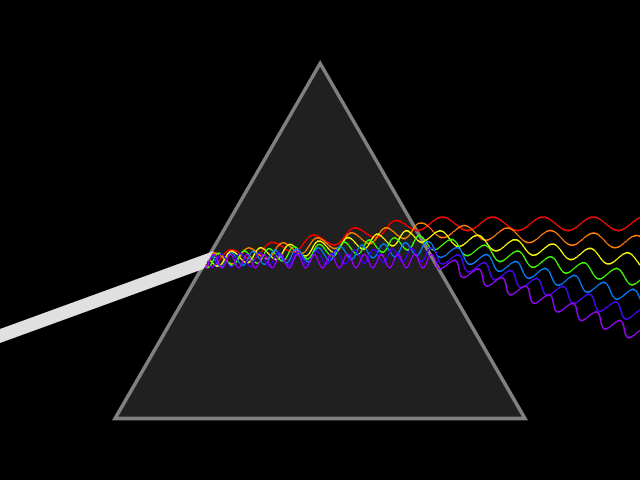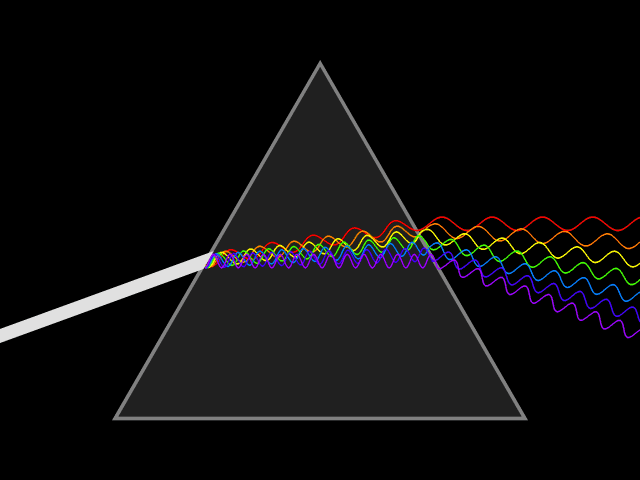
Mimo że światło tworzą cząstki - fotony, to ma ono także naturę fali. Źródło: Wikipedia, domena publiczna
Podobnie Paulowi Diracowi w jednym z równań wyszło, że powinna istnieć cząstka o ujemnej energii. Wydawałoby się, że nie ma to sensu. Dirac jednak wiedział, że poprawnie użył "języka smoków", właściwie sformułował problem i nie popełnił błędu w obliczeniach. To, że tak osobliwe cząstki istnieją, nie mogło być więc w jego ocenie fałszem. W ten sposób przewidział istnienie antymaterii - pozytonów (ślady po przelocie pozytonów obserwować można choćby w komorze mgłowej).
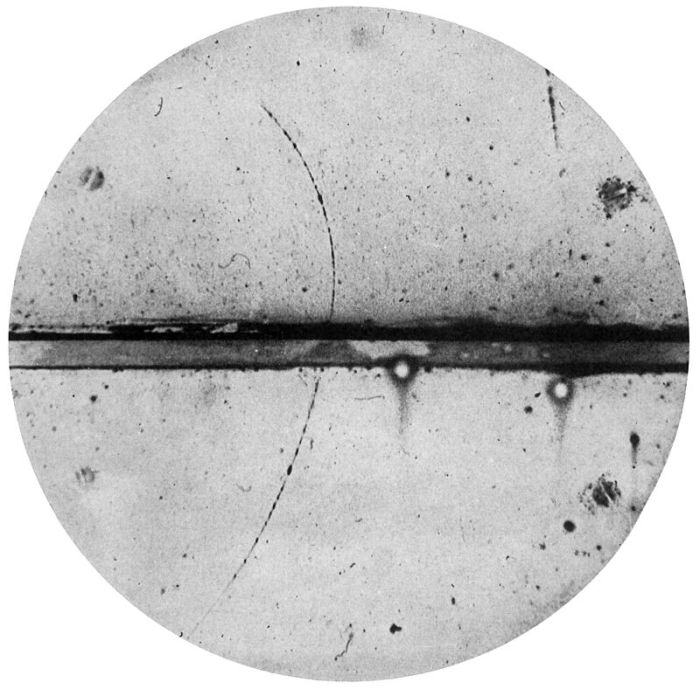
Trajektoria pierwszego odkrytego antyelektronu. Carl D. Anderson (1905–1991) - Anderson, Carl D. (1933). "The Positive Electron". Physical Review 43 (6): 491–494. DOI:10.1103/PhysRev.43.491). Źródło: Wikipedia, domena publiczna
WYZWANIA DLA ZNAWCÓW JĘZYKA SMOKÓW
O różnych problemach można mówić w języku matematyki używając różnych określeń. W "języku smoków" zaczęły się więc z czasem wyłaniać różne dialekty, np. geometria, algebra, topologia, teoria mnogości, równania różniczkowe. Czasami, jeśli przetłumaczy się jakiś problem z jednego dialektu na drugi, a potem - na język potoczny - można zauważyć pewne zależności, które nie były wcześniej widoczne.
Jacek Szczytko zachęca matematyków, by podejmowali trud przekładu tego "języka smoków" na język potoczny. I by inspirowali innych tym, co robi się w matematyce. "Młodzi ludzie, którzy przychodzą do naszych laboratoriów i chcą z nami pracować, robią to zwykle nie dlatego, że spodobało im się jakieś równanie, tylko dlatego, że usłyszeli gdzieś - w języku naturalnym - że to, co robimy jest ciekawe. Uważam, że obowiązkiem naukowców jest więc opowiadanie o `języku smoków` tym, którzy go nie rozumieją" - podsumowuje.
"Język smoków ma swoje ograniczenia - nie można w nim sformułować wszystkich problemów" - przyznaje Jacek Szczytko. Precyzuje, że trudno w nim zawrzeć choćby problemy badawcze związane z badaniem świadomości. Zdaniem naukowca konieczne jest więc rozwijanie wiedzy o tym języku, aby móc stosować go do szukania odpowiedzi na nowe pytania. "Do opisu `niepowtarzalnych` lub `nieobliczalnych` zjawisk potrzebne są jakieś inne metody matematyczne wykraczające poza `zwykłą matematykę`. I to może być niezły program badań naukowych" - mówi dr Szczytko.
Dodaje jednak, że jeśli trzymać się porównania matematyki z językiem smoków, w którym jednak smoki mogą "mówić co chcą" (nie tylko samą prawdę), to w matematyce są zdania poprawne gramatycznie, a których prawdziwości lub fałszywości nie jesteśmy w stanie dowieść. "Mówi o tym twierdzenie Gödla" - dopowiada fizyk. Takie zdania możemy przyjąć za prawdę albo za kłamstwo i w ten subiektywny sposób skonstruować trochę odmienne teorie matematyczne. „Możliwe, że nasz Wszechświat da się opisać tylko jedną z nich, a pozostałe teorie tworzą odmienne światy, których odkrycie będzie niezwykłym osiągnięciem” - powiedział.
***
Dr hab. Jacek Szczytko z zespołem opublikował niedawno artykuł w "Science", w którym - odnosząc się do języka matematyki - fizycy pokazują, jak foton można upodobnić do elektronu.
Fotony i elektrony to zupełnie inne cząstki - jedna porusza się z prędkością światła, nie reaguje na pole elektromagnetyczne i nie ma masy, a jej zadaniem jest przenoszenie oddziaływań. Druga zaś ma dobrze wyznaczoną masę, ładunek i nie osiąga prędkości światła i reaguje na pole elektromagnetyczne. W pewnych jednak warunkach - w dwuwymiarowej przestrzeni - równania opisujące zachowanie fotonu wyglądają jak równania opisujące zachowania masywnego elektronu – np. można taki masywny foton zatrzymać. Wydawałoby się, że przeczy to logice. "Język smoków" i tu pokazuje jednak, że prawdziwe mogą być stwierdzenia, które trudno sobie wyobrazić.
PAP - Nauka w Polsce, Ludwika Tomala
lt/ agt
Przed dodaniem komentarza prosimy o zapoznanie z Regulaminem forum serwisu Nauka w Polsce.